Notes
To edit a note, type text into the Edit box. An image of the Edit box is shown below.
There is a comprehensive help file at the Edit box. Preview this file by clicking on the link below:
HelpTo view the result of your edits, you click on the Save button at the top of the Edit box.
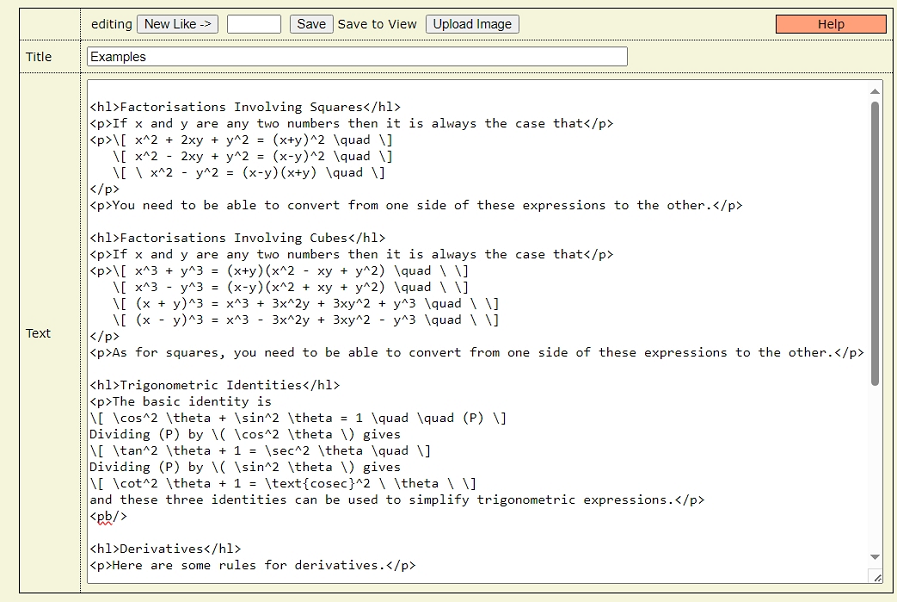
The result looks like this:
Factorisations Involving Squares
If x and y are any two numbers then it is always the case that
\[ x^2 + 2xy + y^2 = (x+y)^2 \quad \] \[ x^2 - 2xy + y^2 = (x-y)^2 \quad \] \[ \ x^2 - y^2 = (x-y)(x+y) \quad \]
You need to be able to convert from one side of these expressions to the other.
Factorisations Involving Cubes
If x and y are any two numbers then it is always the case that
\[ x^3 + y^3 = (x+y)(x^2 - xy + y^2) \quad \ \] \[ x^3 - y^3 = (x-y)(x^2 + xy + y^2) \quad \ \] \[ (x + y)^3 = x^3 + 3x^2y + 3xy^2 + y^3 \quad \ \] \[ (x - y)^3 = x^3 - 3x^2y + 3xy^2 - y^3 \quad \ \]
As for squares, you need to be able to convert from one side of these expressions to the other.
Trigonometric Identities
The basic identity is \[ \cos^2 \theta + \sin^2 \theta = 1 \quad \quad (P) \] Dividing (P) by \( \cos^2 \theta \) gives \[ \tan^2 \theta + 1 = \sec^2 \theta \quad \] Dividing (P) by \( \sin^2 \theta \) gives \[ \cot^2 \theta + 1 = \text{cosec}^2 \ \theta \ \] and these three identities can be used to simplify trigonometric expressions.
Derivatives
Here are some rules for derivatives.
Basic Properties of the Derivative
Since the derivative is defined as a limit, the properties of limits apply:
If \( h(x) = f(x) + g(x) \) then \[ \frac{d}{dx} h(x) = \frac{d}{dx}f(x) + \frac{d}{dx}g(x) \quad \ \] From the limit definition of the derivative. This just reflects the fact that the limit of a sum is the sum of the limits.
If \( h(x) = kf(x) \) for some constant k, then \[ \frac{d}{dx}h(x) = \frac{d}{dx}k f(x) = k \frac{d}{dx}f(x) \quad \ \] This just reflects the fact that a constant can be moved past a limit sign.
Derivative of a Positive Integral Power
If n is a positive integer, then \[ \begin{align} \frac{d}{dx}x^n &= nx^{n-1} \end{align} \ \]