Direction fields

 

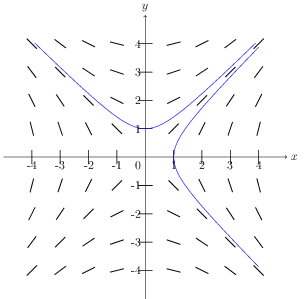
For the differential equation \[ y' = \frac{x}{y} \] (a) Plot a direction field in the rectangle R[\( (-4 \lt x \lt 4 ) \) \( (-4 \lt y \lt 4 ) \)].
(b) Sketch some solution curves on the direction field.

A direction field shows points where \[ y' = \frac{x}{y} = \text{constant} \quad \ \]

Vary x and y to get y' at different points.

Calculate y' at points in the rectangle R.

Here are the values of y' at points in the upper right quadrant.

  

Plot the direction field in the rectangle R.

Here is the plot

  

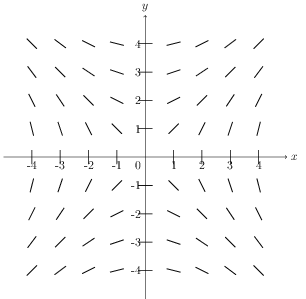
Identify areas of interest on the direction field.

The direction field has

Horizontal tangents on the y axis
Vertical tangents on the x axis
When y > 0, the tangents increase from negative to positive as x increases
When x > 0, the tangents increase from negative to positive as y increases
The tangents converge along the lines y = x, y = -x.

Here are some solution curves:

  

You will gain most benefit if you work through each problem first and then come back and check your work against the solution.

 

y

Now You Try:

For the differential equation \[ y' = -y \] (a) Plot a direction field in the rectangle R[\( (-3 \lt x \lt 3 ) \) \( (-3 \lt y \lt 3 ) \)].
(b) Sketch some solution curves on the direction field.