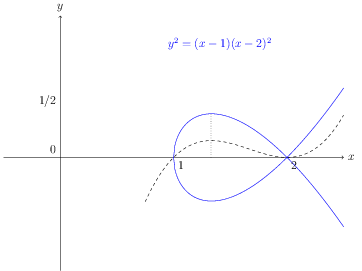Sketch the graph of
\[ y^2 = (x-1)(x-2)^2 \]
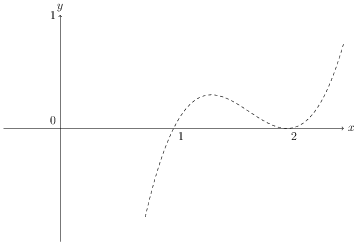
Sketch f(x)
f(x) is a cubic with zeros at x = 1, 2.
Find intercepts of the positive part of y:
\[ y = \pm \sqrt{(x-1)(x-2)^2} \]
So
When x = 0, the positive part of y is not defined (domain of y is \(x \ge 1\))
When y = 0, x = 1 or 2
Find the asymptotes
When x is large and positive, y is large and positive
So no horizontal asymptotes.
y has no vertical asymptotes
Vertical tangents occur when the argument of the square root is about to become negative. These are also the points where f(x) is zero.
For the case at hand, only x = 1 satisfies these two conditions as the square root does not become negative around x = 2. So x = 1 is a vertical tangent.
Estimate the maximum for y in the interval from 1 to 2
An estimate for the maximum is x = 4/3. And at this point, y = 0.385
Now reflect the positive part of y in the x-axis.
Your sketch should look something like this: