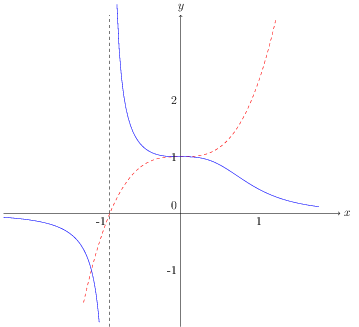
Sketch the graph of
\[ y = \frac{1}{x^3 + 1} \]
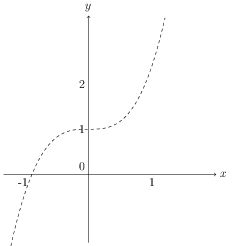
Sketch the inner function
The inner function is a standard cubic shifted one unit in the positive y direction.
Find intercepts of 1/f:
When x = 0, 1/(x3 + 1) = 1
When x3 + 1 = 0, x = -1 so 1/(x3 + 1) is not defined at x = -1
Find the asymptotes
When x is large and positive, 1/(x3 + 1) approaches zero
When x is large and negative, 1/(x3 + 1) approaches zero
So y = o is a horizontal asymptote.
From the intercept analysis, x = -1 is a vertical asymptote
To determine where the two graphs intersect, solve
\[ x^3 + 1 = \frac{1}{x^3 + 1} \]
This gives
\[ \begin{align}
(x^3 + 1)^2 &= 1 \\
x^3 + 1 &= \pm 1 \\
x^3 = 0 \quad &\text{and} \quad x^3 = -2
\end{align} \ \]
so the intersection point is x = 0, y = 1 and x = -1.26, y = -1.
Investigate the point x = 0
When x = -1/2, y = 8/7. When x = -1/4, y = 64/63.
When x = 1/2, y = 8/9. When x = 1/4, y = 64/65.
So the curves becomes horizontal at x = 0.
Your sketch should look something like this: