Discrete probability distribution

 

Z is a random variable that counts the number of heads minus the number of tails on the toss of three fair coins.

(a) Assign a value z to each element of the sample space.
(b) Find the probability distribution of Z.
(c) Confirm that the answer in b is a probability distribution.

Use the rule for Z to assign values to elements of the sample space.

For example, for the outcome HHH, z = 3 - 0 = 3. For the outcome TTH, z = 1 - 2 = -1. Here is the complete table.

  

To find the probability for each value, add the probabilities for each element of the sample space that produces that value.

For example, the probability for the value 1 is the sum of the probabilities for HHT, HTH and THH: \[ \begin{align} \text{P(Z = 1)} &= \text{P(HHT) + P(HTH) + P(THH)} \\ &= \frac{1}{8} + \frac{1}{8} + \frac{1}{8} \\ &= 0.375 \end{align} \ \] Here is the table of probabilities:

  

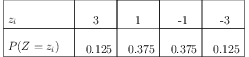
Check the properties of a probability distribution to confirm.

All the probabilities are greater than or equal to zero.
The probabilities sum to 1

So the table does describe a probability distribution.

You will gain most benefit if you work through each problem first and then come back and check your work against the solution.

 

y

Now You Try:

A jar contains four red and six green balls. A ball is drawn from the bag, its colour noted and the ball is replaced. The draw is repeated.

Z is a random variable that counts the number of red balls drawn.

(a) Assign a value z to each element of the sample space.
(b) Find the probability distribution of Z.
(c) Confirm that the answer in (b) is a probability distribution.